Talk:Missing square puzzle

Discoverer for this illusion

Any history or discoverer for this illusion? Ivan 03:16, Feb 21, 2004 (UTC)

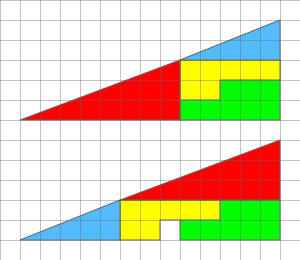
The example of vanishing area puzzles was reported in the book “Libro d’Architettura Primo” by Sebastiano Serlio, an Italian architect of the Renaissance (even though Serlio didn’t notice that any area had actually vanished!). The first description and mathematical explanation of the vanish paradox was found in a math puzzle book with a very long title: “Rational Recreations in which the Principles of Numbers and Natural Philosophy are clearly & copiously elucidated, by a Series of easy, entertaining, interesting Experiments among which are all those commonly performed with the Cards” by William Hooper (1774). - G. Sarcone, source: PUZZILLUSIONS, Archimedes-lab.org, Carlton Books Ltd, ISBN 1844420647 I believe that this was done before Hooper In 1769 Edmé Gilles Guyot (1706-1786) described the vanish area paradox in the second volume of his Nouvelles récréations physiques et mathématiques (both first editions have the same mistake in the problem) Nice puzzle Ed. :-) Perhaps my diagram's too small - it works best when large, I think... Evercat 22:45, 13 Nov 2003 (UTC)

Just perfect, kittie-cat. Meow! Thanks for the verbal and graphic clarifications. Now let's fix global warming, okay? ;-) --Uncle Ed 14:49, 14 Nov 2003 (UTC)

Curry's paradox

The lead relates that the paradow has been attributed to Paul Curry. Then, it stated:

Ever since, it has been known as Curry's paradox.

But an editor changed this into

Ever since, it has not been known as Curry's paradox because of a paradox of a similar name.

Clearly, Curry's paradox is unrelated. I have removed both versions, pending a source clearing this up.--Noe (talk) 06:49, 21 April 2008 (UTC)

redirected Vanishing area parodox here

Martin Gardner, amongst others, calls this the "Vanishing area paradox", so I created that page as a redirect to this one. (And curiously Google ranks this page as the #2 search result for 'vanishing area parodox' even though the phrase doesn't appear in the article.)Loren Rosen (talk) 21:36, 28 November 2008 (UTC)

Sam Lyod's dissection Paradox

I still don't understand this paradox. If the surface area of each individual shape is measured, the two triangles are 12 units each, and the two trapezoids are 20 units each, which equals 64 squared units in total surface area. When the pieces are arranged into a rectangle, the surface area is 65 squared units, although it contains two triangles of 12 and 2 trapezoids of 20 which still equals 64 squared units. How did that magical 1 squared unit appear?

You forgot to sign your post. In the 5X13 rectangle, the pieces don't actually fit together in the grid. If you look at the right edge of the purple triangle, it is three units in length, but the green triangle does not actually fill the rest of the five units; it is actually 1 7/8 units wide at that point. In other words, if the top and bottom edges of the rectangle are on the grid lines, what appears to be a diagonal is actually a long, thin quadrilateral (actually a parallelogram)with area 1.

In the diagram having a supposed area of 63, the edges of the diagram cannot actually be on the grid lines unless the pieces overlap. For example the right edge of the peach-colored piece is five units long, while the width of the green triangle at that point is 9/8 units, so to fit them onto the grid, you have to overlap them by an eighth of a unit. The "diagonal" is the same parallelogram as before, but now it's an area of overlap rather than a space.--Syd Henderson (talk) 22:20, 6 May 2010 (UTC)

The text following "forgot to sign your post" has apparently caused this page to be about 3 times W I D E R than normal. Can someone fix this?Racerx11 (talk) 00:17, 31 August 2010 (UTC)

Done. –Schmloof (talk · contribs) 00:33, 31 August 2010 (UTC)

That was quick, ThanksRacerx11 (talk) 02:36, 31 August 2010 (UTC)

Bent Hypotenuse

If the "hypotenuse" is actually not a straight line, doesn't that make the final shape a quadrilateral? --Thegargoylevine (talk) 02:58, 6 May 2010 (UTC)

It does indeed! Schmloof (talk) 02:17, 7 May 2010 (UTC)

File:Missing square puzzle.svg to appear as POTD

Hello! This is a note to let the editors of this article know that File:Missing square puzzle.svg will be appearing as picture of the day on March 9, 2013. You can view and edit the POTD blurb at Template:POTD/2013-03-09. If this article needs any attention or maintenance, it would be preferable if that could be done before its appearance on the Main Page. Thanks! — Crisco 1492 (talk) 05:37, 23 February 2013 (UTC)

Picture of the day

The missing square puzzle is an optical illusion used in mathematics classes to help students reason about geometrical figures. It depicts two arrangements of shapes, each of which apparently forms a 13×5 right-angled triangle, but one of which has a 1×1 hole in it.Picture: Fibonacci

Further application

See this x3 application and videos. Yug (talk) 11:46, 9 April 2013 (UTC)

Infinite Chocolate

My daughter was distressed by an animation that supposedly shows how you can infinitely remove one chunk of chocolate from a bar and rearrange it to get a whole new bar. Some sketches suggest the answer is that the shapes don't really fit as they are drawn, just as in this puzzle. What looks like a straight break across the bar is presumably bent. If so then perhaps the chocolate puzzle (which seems to have become an internet [meme] should be referenced in this article? — Preceding unsigned comment added by 95.148.251.105 (talk) 19:35, 23 April 2013 (UTC)

FYI I've seen the chocolate bar you're talking about; the trick in that one is that the size of the bar subtly changes as the pieces move around - i.e. the video is somewhat doctored. The size of the squares in the bar "grow" after it's cut into pieces, so that it takes up the same amount of space after removing a piece. -Hatster301 (talk) 16:03, 24 April 2013 (UTC)

Removed link

I removed a link to a video by Azulejos Jansenson. At first glance, this video looks like a variant of the missing square puzzle, but the effect seems to be accomplished in part by editing the video to unobtrusively substitute a different set of pieces. If I am correct, it is neither an optical illusion nor a legitimate puzzle, but a "camera trick", and therefore doesn't belong here. --N Shar (talk · contribs) 06:38, 9 July 2013 (UTC)

I agree; the video is definitely edited, and pieces are surreptitiously switched during non-contiguous transitions. For example, look at the size and shape of the squares when the pieces are inside the frame at 2:15. Then, after the pieces are removed and laid out on the table (2:35), it is clear that the squares no longer display the same uniformity, especially those along the "crack" across the middle; some are elongated taller, while some are smushed shorter, clearly indicating that the pieces laid out on the table are not the same pieces that had previously been inside the frame.

Easier-To-Understand Demo Request

It would be great to see an animation that takes this a little further to make it easier to see--if the hypotenuse were bent enough to lose two squares after the transition, our eyes would be able to see what's happening here quite easily. — Preceding unsigned comment added by 66.65.165.172 (talk) 04:29, 25 July 2014 (UTC)

Another version - what sorcery is this?

There's a gif floating around that doesn't just do one magical piece, it does it twice AND puts the pieces back into a frame showing that the entire puzzle neither grew nor shrank. I'll link it here for discussion, rather than on the page because, while it's different enough, I can't find an original video source that doesn't eliminate camera tricks. https://www.gif-vif.com/gifs/What-sorcery-is-this-115/ --Snicker^|¥°^€| 07:15, 3 April 2020 (UTC)